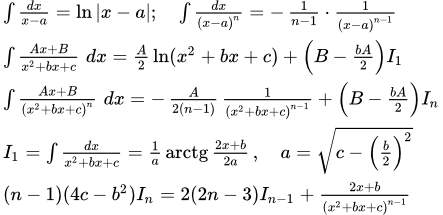Решим квадратное уравнение: $$ x^2+5x-6 = 0 $$
С учётом полученных корней, преобразуем интеграл:
Выполняем разложение рациональной дроби:
Приравниваем числители и находим коэффициенты $ A $ и $ B $:
$$ Ax + 6A + Bx — B = x + 2 $$
$$ �egin A + B = 1 \ 6A — B = 2 end $$
Подставляем в интеграл найденные коэффициенты и решаем его:
Метод интегрирования, при котором интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием. См. Таблица интегралов.
Подведение под знак дифференциала
Данный метод эквивалентен методу замены переменной (см. далее).
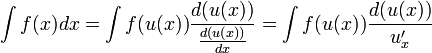
Метод замены переменной (метод подстановки)
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть требуется вычислить интеграл 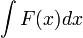 . Сделаем подстановку
. Сделаем подстановку 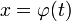 , где
, где 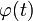 — функция, имеющая непрерывную производную.
— функция, имеющая непрерывную производную.
Тогда 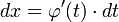 и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:
и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:
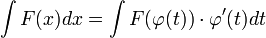
Интегрирование выражений вида 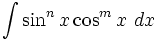
Если m = 2k + 1,m > 0 , то удобнее сделать подстановку sin x = t
Если n = 2k + 1,n > 0 , то удобнее сделать подстановку cos x = t
Примеры
Вычислить: 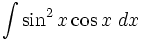 Пусть sinx = t , тогда
Пусть sinx = t , тогда 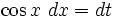
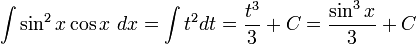
Интегрирование по частям
Интегрирование по частям — применение следующей формулы для интегрирования:
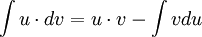
С помощью n-кратного применения этой формулы находится интеграл
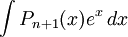 ,
,
Интегрирование рациональных дробей
Неопределенный интеграл от любой рациональной дроби на всяком промежутке, на котором знаменатель дроби не обращается в нуль, существует и выражается через элементарные функции, а именно он является алгебраической суммой суперпозиции рациональных дробей, арктангенсов и рациональных логарифмов.
Сам метод заключается в разложении рациональной дроби на сумму простейших.
Всякую правильную рациональную дробь 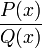 , знаменатель которой разложен на множители
, знаменатель которой разложен на множители
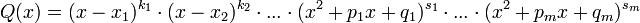 можно представить (и притом единственным образом) в виде следующей суммы простейших дробей:
можно представить (и притом единственным образом) в виде следующей суммы простейших дробей: 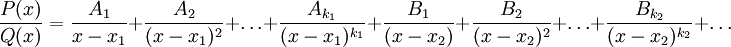
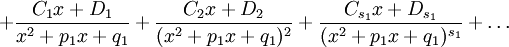
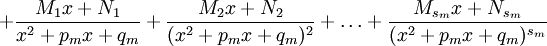
где 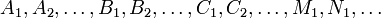 — некоторые действительные коэффициенты. Обычно неизвестные коэффициенты находятся с помощью метода неопределённых коэффициентов.
— некоторые действительные коэффициенты. Обычно неизвестные коэффициенты находятся с помощью метода неопределённых коэффициентов.
См. также
Wikimedia Foundation . 2010 .
Смотреть что такое "Интегрирование рациональных дробей" в других словарях:
Методы интегрирования — Точное нахождение первообразной (или интеграла) произвольных функций дело гораздо более сложное, чем дифференцирование, то есть нахождение производной. Зачастую выразить интеграл в элементарных функциях невозможно. Содержание 1… … Википедия
Бугаев Николай Васильевич — Бугаев (Николай Васильевич) заслуженный ординарный профессор математики Московского университета, родился в 1837 г. в Душете (Тифлисской губернии), где получил первоначальное образование, а в 1847 г. был отправлен своим отцом, военным врачом… … Биографический словарь
Бугаев, Николай Васильевич — заслуженный ординарный профессор математики Московского университета; родился 1837 г. в Душете (Тифлисской губ.), где получил первоначальное образование, а в 1847 г. был отправлен своим отцом, военным врачом кавказских войск, во 2 ю московскую… … Большая биографическая энциклопедия
Бугаев — (Николай Васильевич) заслуженный ординарный профессор математики Московского университета, родился 1837 г. в Душете (Тифлисской губ.), где получил первоначальное образование, а в 1847 г. был отправлен своим отцом, военным врачом кавказских войск … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Бугаев Николай Васильевич — I заслуженный ординарный профессор математики Московского университета, родился 1837 г. в Душете (Тифлисской губ.), где получил первоначальное образование, а в 1847 г. был отправлен своим отцом, военным врачом кавказских войск, во 2 ю московскую… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Бугаев, Николай Васильевич — В Википедии есть статьи о других людях с такой фамилией, см. Бугаев. Николай Васильевич Бугаев … Википедия
Перевощиков, Димитрий Матвеевич — математик, писатель, экстраординарный академик Императорской Академии Наук, брат Василия Матвеевича Перевощикова; родился 17 го апреля 1788 г. по одним известиям в г. Саранске, а по другим в Шишкееве (теперь заштатном городе) Пензенской губернии … Большая биографическая энциклопедия
Первообразная — Первообразной[1] или примитивной функцией (иногда называют также антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении… … Википедия
Неопределенный интеграл — В математическом анализе первообразной (первообразной) или примитивной функцией данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F′ = f. Вычисление первообразной заключается в нахождении… … Википедия
Певообразная — В математическом анализе первообразной (первообразной) или примитивной функцией данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F′ = f. Вычисление первообразной заключается в нахождении… … Википедия
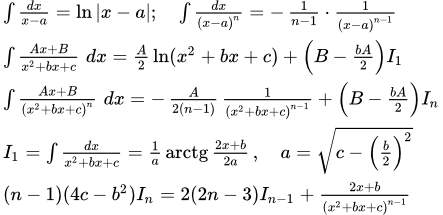
Как известно, любую рациональную функцию от некоторой переменной x можно разложить на многочлен и простейшие, элементарные, дроби. Имеется четыре типа простейших дробей:
1) ;
2) ;
3) ;
4) .
Здесь a, A, B, b, c – действительные числа. Уравнение x 2 + bx + c = 0 не имеет действительных корней.
Интегрирование дробей первых двух типов
Интегрирование первых двух дробей выполняется с помощью следующих формул из таблицы интегралов:
,
, n ≠ – 1 .
1. Интегрирование дроби первого типа
Дробь первого типа подстановкой t = x – a приводится к табличному интегралу:
.
2. Интегрирование дроби второго типа
Дробь второго типа приводится к табличному интегралу той же подстановкой t = x – a :
.
3. Интегрирование дроби третьего типа
Рассмотрим интеграл от дроби третьего типа:
.
Будем вычислять его в два приема.
3.1. Шаг 1. Выделим в числителе производную знаменателя
Выделим в числителе дроби производную от знаменателя. Обозначим: u = x 2 + bx + c . Дифференцируем: u′ = 2 x + b . Тогда
;
.
Но
.
Мы опустили знак модуля, поскольку .
3.2. Шаг 2. Вычисляем интеграл с A = 0, B=1
Теперь вычисляем оставшийся интеграл:
.
Приводим знаменатель дроби к сумме квадратов:
,
где .
Мы считаем, что уравнение x 2 + bx + c = 0 не имеет корней. Поэтому left( frac2
ight)^2" style="width:88px;height:51px;vertical-align:-24px;background-position: -0px -156px;"> .
Тем самым мы нашли интеграл от дроби третьего типа:
,
где .
4. Интегрирование дроби четвертого типа
И наконец, рассмотрим интеграл от дроби четвертого типа:
.
Вычисляем его в три приема.
4.1) Выделяем в числителе производную знаменателя:
.
4.2) Вычисляем интеграл
.
4.3) Вычисляем интегралы
,
используя формулу приведения:
.
Далее мы приводим вывод этих формул, и пример вычисления интеграла от элементарной дроби четвертого типа.
4.1. Шаг 1. Выделение в числителе производной знаменателя
Выделим в числителе производную знаменателя, как мы это делали в разделе 3.1 ⇑. Обозначим u = x 2 + bx + c . Дифференцируем: u′ = 2 x + b . Тогда
.
4.2. Шаг 2. Вычисление интеграла с n = 1
Вычисляем интеграл
.
Его вычисление изложено в разделе 3.2 ⇑.
4.3. Шаг 3. Вывод формулы приведения
Теперь рассмотрим интеграл
.
Приводим квадратный трехчлен к сумме квадратов:
.
Здесь .
Делаем подстановку.
.
.
Выполняем преобразования и интегрируем по частям.
.
Итак, для In мы получили формулу приведения:
.
Последовательно применяя эту формулу, мы сведем интеграл In к I 1 .
Пример
1. Выделим в числителе производную знаменателя.
;
;
.
Здесь
.
2. Вычисляем интеграл от самой простой дроби.
.
3. Применяем формулу приведения:
для интеграла .
В нашем случае b = 1 , c = 1 , 4 c – b 2 = 3 . Выписываем эту формулу для n = 2 и n = 3 :
;
.
Отсюда
.
Окончательно имеем:
.
Находим коэффициент при .
.
Автор: Олег Одинцов . Опубликовано: 09-04-2015 Изменено: 28-01-2018
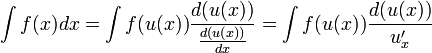
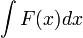 . Сделаем подстановку
. Сделаем подстановку 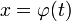 , где
, где 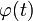 — функция, имеющая непрерывную производную.
— функция, имеющая непрерывную производную.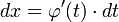 и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:
и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой: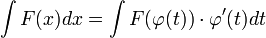
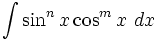
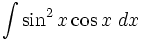 Пусть sinx = t , тогда
Пусть sinx = t , тогда 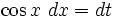
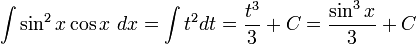
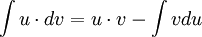
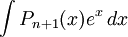 ,
,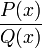 , знаменатель которой разложен на множители
, знаменатель которой разложен на множители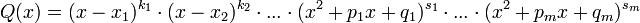 можно представить (и притом единственным образом) в виде следующей суммы простейших дробей:
можно представить (и притом единственным образом) в виде следующей суммы простейших дробей: 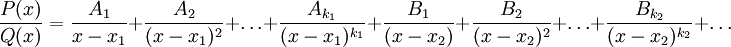
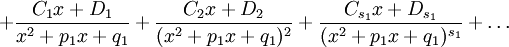
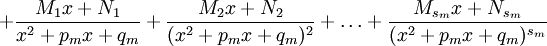
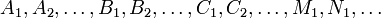 — некоторые действительные коэффициенты. Обычно неизвестные коэффициенты находятся с помощью метода неопределённых коэффициентов.
— некоторые действительные коэффициенты. Обычно неизвестные коэффициенты находятся с помощью метода неопределённых коэффициентов.